R语言线性回归
发布于 2016-01-02 09:30:57 | 964 次阅读 | 评论: 2 | 来源: 网络整理
回归分析是一种应用非常广泛的统计工具来建立两个变量之间的关系模型。其中一个变量被称为预测变量,其值是通过实验收集的。另一变量称为响应变量,其值是从预测变量而得。
线性回归这两个变量是通过一个等式,其中这两个变量指数(幂)为1有关。 在数学上线性关系表示直线时为图形。非线性关系,其中任何一个变量的指数不等于1创建曲线。线性回归的一般数学方程为:
y = ax+b
以下是所使用的参数的说明:
- y 是响应变量
- x 是预测变量
- a 和 b 称为系数常数
建立回归步骤
回归的一个简单的例子是一个人的预测体重时,身高是已知的。要做到这一点,我们需要有一个人身高和体重之间的关系。
创建关系的步骤是:
- 进行收集身高观测值的一个样本和相应的权重的实验
- 使用 lm() 函数在R创建关系模型
- 找到从所创建的模型的系数和使用这些创建的数学方程
- 获取关系模式的总结,以知道在预测也称残值的平均误差
- 预测新的人重量,使用 R 的 predict()函数
示例
输入数据
下面是代表观测样本数据:
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48
lm() 函数
这个函数创建来预测和响应变量之间的关系模型。
语法
下面是 lm() 函数的线性回归的基本语法:
lm(formula,data)
以下是所使用的参数的说明:
- formula 是一个符号呈递x和y之间的关系。
- data 是在其公式将被应用的向量。
创建关系模型及获得系数
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)
当我们上面的代码执行时,它产生以下结果:
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746
获取相关的概要
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))
当我们上面的代码执行时,它产生以下结果:
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06
predict() 函数
语法
对于 predict()在线性回归的基本语法是:
predict(object, newdata)
以下是所使用的参数的说明:
- object 使用 lm()函数创建公式。
- newdata 是向量包含预测变量的新值。
预测的新的人的重量
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x=170)
result <- predict(relation,a)
print(result)
当我们上面的代码执行时,它产生以下结果:
1
76.22869
可视化的回归图形
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
plot(y,x,col="blue",main="Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch=16,xlab="Weight in Kg",ylab="Height in cm")
# Save the file.
dev.off()
当我们上面的代码执行时,它产生以下结果:
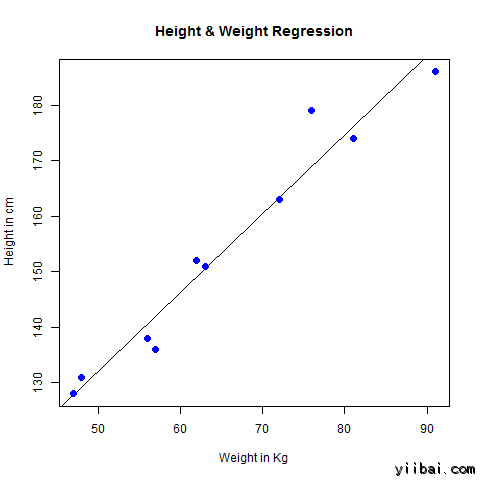
一些简单统计量,回归模型系数最小二乘解以及它们的检验结果。建议专门看一下回归分析的书,人民大学的不错。